|
| |||||||
| Kayıt ol | Yardım | Üye Listesi | Ajanda | Arama | Bugünki Mesajlar | Bütün Forumları okunmuş kabul et |
| Matematik - Geometri Matematik ödevleri,Geometri ödevleri... |
 | ||

 |
| | LinkBack | Seçenekler |
| | #1 (permalink) | ||
| Digama Fonksiyonu Matematik'te, digama fonksiyonu gama fonksiyonu'nun logaritmik türevi olarak tanımlanır:  Bu poligama fonksiyonu'nun ilkidir. 
Digamma fonksiyon'u, sıklıkla ψ0(x), ψ0(x) veya  (eski yunan harfleriyle digama'nın gösterimi Ϝ'dir ) şeklinde gösterilir. Harmonik sayılar'la ilişkisi (eski yunan harfleriyle digama'nın gösterimi Ϝ'dir ) şeklinde gösterilir. Harmonik sayılar'la ilişkisi Burada Hn is the n 'inci harmonik sayıdır, ve γ Euler-Mascheroni sabiti'dir. yarı tamsayı değerleri için, açılım 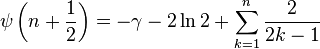 Integral Gösterimleri integral gösterimi  şeklindedir. şeklindedir.x reel kısmının pozitif değerleri için geçerlidir.Bunu şöyle yazabiliriz  harmonik sayılar için Euler integrali'dir . Seri formülü Digamma negatif tamsayılar dışında kompleks düzlemde hesaplanabilir (Abramowitz and Stegun 6.3.16), yardımıyla  Taylor serisi Digama Taylor serisi'nde z=1 verilerek elde edilen bir rasyonel zeta serisidir , . Burada  yakınsaklık için |z|<1. Burada, ζ(n) Riemann zeta fonksiyonu'dur.Bu seri ile kolayca Hurwitz zeta fonksiyonu'na karşılık gelen Taylor 'serisi elde edilebilir. Newton serisi Digama için Newton serisi Euler integral formulü ile : 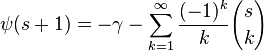 Burada  binom katsayısı'dır binom katsayısı'dırRefleksiyon formülü Digama fonksiyonunu Gama fonksiyonu'na benzer bir refleksiyon formülü karşılar  Özyineleme formülü tekrarlama ilişkisi'ne dayanılarak Digamma fonksiyonu  Böylece,1/x için "teleskop" denilebilir , bu nedenle  Burada Δ ileri diferansiyel operator'dür. Aşağıdaki formülle harmonik seri'nin kısmi toplamı tekrarlama ilişkisi'ne karşı gelir ,  burada  Euler-Mascheroni sabiti'dir. Euler-Mascheroni sabiti'dir.Daha genel bir ifade,  Gauss toplamı Digama'nın Gaussian toplam formu 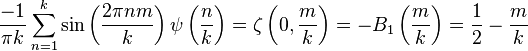 Tamsayılar için 0 < m < k. Burada, ζ(s,q) Hurwitz zeta fonksiyonu'dur ve Bn(x) 'i Bernoulli polinomu'dur.Çarpma teoremi'nin özel bir durumu ;  ve genelleştirilmiş şekli  Burada q 'nun doğal sayı, ve 1-qa 'nın doğal sayı olmadığı varsayılmıştır. . Gauss'un digama teoremi [ Pozitif tamsayılar m ve k ( m < k ) şartıyla,digama fonksiyonunun Temel fonksiyon olarak ifadesi  Hesaplama & yaklaşıklık J.M. Bernardo AS 103 algoritmiyle ile x, gerçel bir sayı olmak üzere digama fonksiyonu hesaplanabilir,  veya veya  n tamsayı, B(n) n 'inci Bernouilli sayısı ve ζ(n) Riemann zeta fonksiyonu'dur. Özel değerler Digama fonksiyonu için bazı özel değerler: 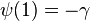      --------------Tualimforum İmzam-------------- Aksini Belirtmediğim Takdirde Yazdığım Konular ALINTIDIR Liseler - Anadolu Liseleri - Fen Liseleri Anaokulu - İlköğretim Sınav Soruları ve Ders Notları | |||
| |  |