Gama Fonksiyonu
Gama fonksiyonu Matematikte faktöriyel fonksiyonunun karmaşık sayılar ve tam sayı olmayan reel sayılar için genellenmesi olan bir fonksiyondur. Г simgesiyle gösterilir.
Kompleks düzlemde Analitik devamlılık için n negatif tamsayı olmamalıdır,pozitif tamsayı olmalıdır.
- Reel eksen boyunca gama fonksiyonu
Alıştırma
Öncelikle
(n + 1)n! = (n + 1)! eşitliğini ele alalım,n = 0'alırsak
1.1! = 0! = 1 olur.
aynı işlem kesirli sayılarla yapılabilirmi? diye bir soru akla gelir.
n = 1 / 2 alırsak;
(3 / 2)(1 / 2)! = (3 / 2)!,olması gerekir.Yani
(3 / 2)(1 / 2)! = (3 / 2)!→(3 / 2)! / (1 / 2)! = 3 / 2'olmalıdır
Γ(n) = (n − 1)!' olduğundan;
Γ(5 / 2)→(3 / 2)! 'ye karşılık gelmelidir(eşittir demiyoruz) ve yine
Γ(3 / 2)→(1 / 2)! işlemine karşılık gelmelidir.
Γ(5 / 2) / Γ(3 / 2) = 3 / 2
Buda
Γ(5 / 2) / Γ(3 / 2) = 3 / 2→(3 / 2)! / (1 / 2)! = 3 / 2 varsayımımızı doğruluyor.Denenirse diğer sayılar içinde bunun doğruluğu görülebilir.
Tanım
Ana Tanı
Bu çift Γ(z) gösterim Legendre tarafından yapılmıştır.kompleks sayı z'nin gerçel kısmı (Re[z] > 0) şeklindedir. integral'i
Burada kısmi integrasyon kullanarak, mutlak yakınsaklık gösterilebilir.
n ! = n · (n − 1) ! faktoriyel fonksiyonunun genel kimliği/tanımı Bu fonksiyonel denklemdir.
Bu iki sonuç bize faktöriyel fonksiyonun gama fonksiyonun özel bir durumu olduğunu gösteriyor. Bütün n Doğal sayılar'ı için .
Γ(z) genellemesi analitik devamlılık için gereklidir.z böylece 0 ve negatif değerler hariç bütün kompleks sayıları meromorfik fonksiyon olarak tanımlar., ( z. = −nbasit kutbu ile rezidü (−1) n/n !).
Alternatif tanımlamalar
0 ve negatif tamsayılar dışında bütün kompleks sayılar z için tanım sonsuz sayıda Gama fonksiyonu için, sırasıyla Euler ve Weierstrass çifti tarafından
burada γ, Euler-Mascheroni sabiti'dir.
yukarıdaki z nin 0,-1,-2,-3..dışındaki değerleri için Euler tanımı fonksiyonel denklemi basitleştirilmiş şekli,
değişik bir gösterim...
Bazen Gamma fonksiyonu'nun parametrik şekli Laguerre polinomları'nın terimleri içinde verilir;
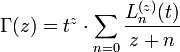 yakınsaklık için
yakınsaklık için  olmalıdır.
olmalıdır. Mutlak değer
Mutlak değer Gerçel kısım
Gerçel kısım Hayali kısım
Hayali kısımÖzel değerler









 Benzer Konular
Benzer Konular