 |
| |||||||
| Kayıt ol | Yardım | Üye Listesi | Ajanda | Bugünki Mesajlar | Arama |
| Elektronik-Bilgisayar Elektronik ödevleri,Bilgisayar ödevleri... |
 | ||

 |
| | LinkBack | Seçenekler |
 |
| |||||||
| Kayıt ol | Yardım | Üye Listesi | Ajanda | Bugünki Mesajlar | Arama |
| Elektronik-Bilgisayar Elektronik ödevleri,Bilgisayar ödevleri... |
 | ||

 |
| | LinkBack | Seçenekler |
| | #2 (permalink) |
| Delta Üye  Üyelik tarihi: Jan 2008 Nerden: SaMSuN
Mesajlar: 776
Konular: 146 Rep Puanı:1997 Rep Gücü:0 RD:            Ettiği Teşekkür: 0 17 Mesajına 80 Kere Teşekkür Edlidi : | BİRLEŞME KANUNU (ASSOCİATİVE LAWS) Boolean toplama işlemine ilişkin birleşme kanunu A,B,C giriş değişkenlerini göstermek üzere aşağıdaki gibi yazılır.  DAĞILMA KANUNU (DISTRIBUTIVE LAW) A,B,C giriş değişkenlerini göstermek üzere dağılma kanunu aşağıdaki gibi yazılır.  DAĞILMA KANUNU (DISTRIBUTIVE LAW) A,B,C giriş değişkenlerini göstermek üzere dağılma kanunu aşağıdaki gibi yazılır. 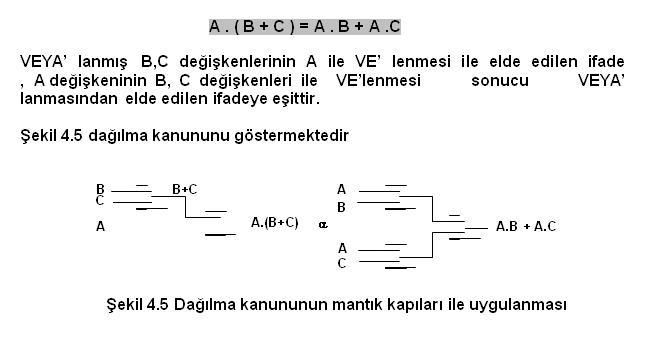 |
| |  |
| | #3 (permalink) |
| Delta Üye  Üyelik tarihi: Jan 2008 Nerden: SaMSuN
Mesajlar: 776
Konular: 146 Rep Puanı:1997 Rep Gücü:0 RD:            Ettiği Teşekkür: 0 17 Mesajına 80 Kere Teşekkür Edlidi : | BOOLEAN MATEMATİĞİ KURALLARI  Kural 1- VEYA özdeşlikleri a) Bir VEYA kapısının girişlerinden biri “0” ise çıkış ifadesi A’ nın durumuna bağlıdır. Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur. b) Bir VEYA kapısının girişlerinden biri “1” ise , A’ nın durumu ne olursa olsun çıkış daima “1” olur. c) Bir VEYA kapısının girişlerine değişkenin değili ile kendisi uygulanırsa çıkış A’nın durumu ne olursa olsun daima “1” olur. d) Bir VEYA kapısının her iki girişine aynı değişken uygulanırsa çıkış A’nın durumuna bağlıdır. Eğer A=0 ise çıkış “0”, =1 ise çıkış “1” olur.  Kural 2- VE özdeşlikleri a) Bir VE kapısının girişlerinden biri “0” ise, A’ nın durumu ne olursa olsun çıkış daima “0”olur. b) Bir VE kapısının girişlerinden biri “1” ise çıkış ifadesi A’ nın durumuna bağlıdır. Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur. c) Bir VE kapısının girişlerine değişkenin değili(tümleyeni) ile kendisi uygulanırsa çıkış A’nın durumu ne olursa olsun daima “0” olur. d) Bir VE kapısının her iki girişine aynı değişken uygulanırsa çıkış A’nın durumuna bağlıdır. Eğer A=0 ise çıkış “0”, A=1 ise çıkış “1” olur 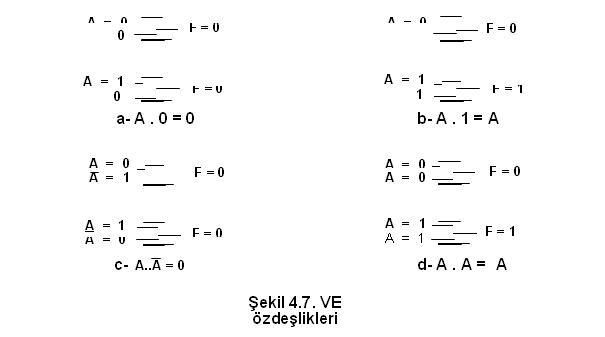 Kural 3- Çift tersleme kuralı Bir Lojik ifadenin veya değişkenin iki defa değili alınırsa (terslenirse) lojik ifadenin veya değişkenin aslı elde edilir 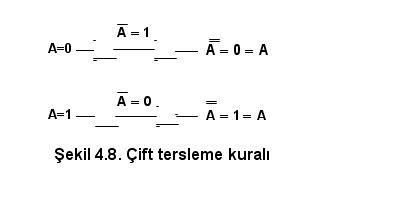 Kural 4- Yutma kuralı Bu kuralı dağılma kanunu ve VEYA, VE özdeşlikleri yardımı ile açıklayalım. Eğer ifadeyi A ortak paranaaaine alırsak aşağıdaki dönüşüm sağlanmış olur.  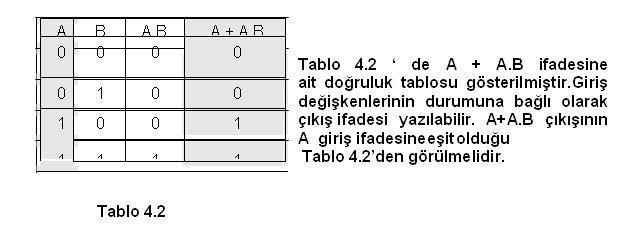 Kural 5  Kural 6 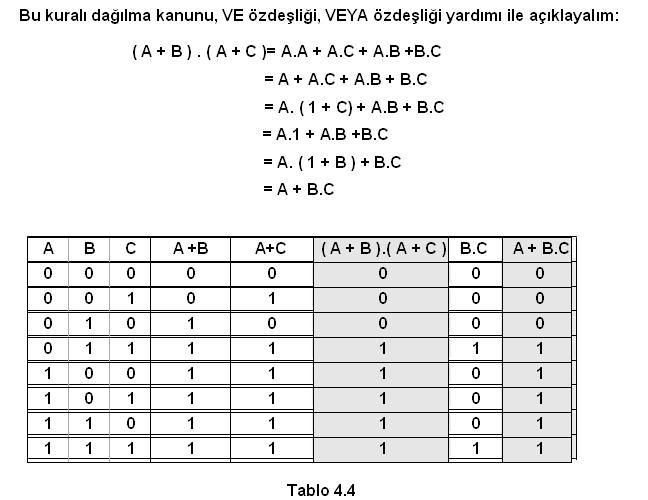 Tablo 4.4’de girişlerin durumuna bağlı olarak ( A + B) . ( A + C ) ile A + B.C ifadelerinin durumları yazılmıştır. Bu iki ifadenin eşitliği tablodan görülebilir. |
| |  |
 |
| Tags |
| boolean, matematigi, ozellikleri, ve |
| Konuyu Toplam 1 Üye okuyor. (0 Kayıtlı üye ve 1 Misafir) | |
| |
 Benzer Konular
Benzer Konular | ||||
| Konu | Konuyu Başlatan | Forum | Cevaplar | son Mesaj |
| Sony DSC WX5 Dijital Fotoğraf Makinesi Özellikleri - Sony DSC WX5 Ürün Özellikleri | Kartal | Sony Ericsson | 0 | 17.03.11 12:59 |
| Olympus FE 47 Dijital Fotoğraf Makinesi Özellikleri - Olympus FE 47 Ürün Özellikleri | Kartal | Olympus | 0 | 16.03.11 16:14 |
| Güzelliğin Matematiği | AnGeL | Ağız ve Diş Hastalıkları | 1 | 07.12.10 18:29 |
| Piranaların Özellikleri - Piranhaların Özellikleri | Fenci | Balıklar | 0 | 03.04.10 00:19 |
| Tüm Lise Matematiği | SERDEM | Matematik - Geometri | 0 | 23.08.08 06:29 |