|
| |||||||
| Kayıt ol | Yardım | Üye Listesi | Ajanda | Bugünki Mesajlar | Arama |
| Matematik - Geometri Matematik ödevleri,Geometri ödevleri... |
 | ||

 |
| | LinkBack  | Seçenekler  |
| | #1 (permalink) | ||
| Binom Dönüşümü Nedir - Binom Dönüşümü Tanımı - Binom Dönüşümü Hakkında Tümleşik matematikte binom dönüşümü bir dizinin ileri farklarını hesaplamaya yarayan bir dizi dönüşümüdür. Kavram, binom dönüşümünün Euler dizisine uygulanması sonucu oluşan Euler dönüşümüyle yakından ilintilidir. Tanım Bir {an} dizisinin binom dönüşümü (T)  olarak tanımlanan {sn} dizisidir. olarak tanımlanan {sn} dizisidir.(Ta)n = sn yazımında T bir sonsuz boyutlu işleci göstermektedir. Bu işlecin elemanları şu biçimde gösterilebilir:  Bu dönüşüm bir kıvrılmadır. Bu dönüşüm bir kıvrılmadır.TT = 1 Bu, farklı bir biçimde de gösterilebilir.  Burada δ Kronecker delta işlevini göstermektedir. Burada δ Kronecker delta işlevini göstermektedir. işlemiyle özgün diziye geri dönülebilir. işlemiyle özgün diziye geri dönülebilir.Bir dizinin binom dönüşümü o dizinin n. ileri farkıdır. s0 = a0     Burada Δ ileri fark işlecini simgelemektedir. Burada Δ ileri fark işlecini simgelemektedir.Binom dönüşümü zaman zaman ek bir imle gösterilmektedir. Bu gösterimde dönüşüm  biçiminde ifade edilirken bu ifadenin tersi biçiminde ifade edilirken bu ifadenin tersi olarak yazılır. olarak yazılır.Örnek Binom dönüşümleri fark tablolarında kolaylıkla gözlenebilmektedir. 0 1 10 63 324 1485 1 9 53 261 1161 8 44 208 900 36 164 692 128 528 400 0, 1, 10, 63, 324, 1485, … biçimindeki en üst satır ((2n2 + n)3n − 2 tarafından tanımlanan bir dizi) 0, 1, 8, 36, 128, 400, … köşegeninin (n22n − 1 tarafından tanımlanan bir dizi) binom dönüşümüdür. Değişim durumları Binom dönüşümü Bell sayılarının değişim işlecidir. Başka bir deyişle,  eşitliği sağlanmaktadır. Burada Bn Bell sayılarını göstermektedir. Olağan üretici işlev Dönüşüm, diziyle ilişkilendirilmiş üretici işlevleri birbirine bağlamaktadır. Olağan üretici işlev için  ve ve eşitliklerinin sağlandığı varsayılsın. eşitliklerinin sağlandığı varsayılsın. Buradan  ifadesine ulaşılabilir. ifadesine ulaşılabilir.Euler dönüşümü Olağan üretici işlevler arasındaki ilişki zaman zaman Euler dönüşümü olarak adlandırılmaktadır. İki farklı biçimde var olan dönüşüm, almaşık dizilerin yakınsaklığını hızlandırabilmektedir. Başka bir deyişle,  ifadesinde x yerine 1/2 konularak 1'e ulaşılabilir. Sağdaki terimler çok hızlı bir biçimde küçüldüklerinden bu toplam kolaylıkla hesaplanabilir. ifadesinde x yerine 1/2 konularak 1'e ulaşılabilir. Sağdaki terimler çok hızlı bir biçimde küçüldüklerinden bu toplam kolaylıkla hesaplanabilir.Euler dönüşümü şu biçimde genellenbilir: p = 0, 1, 2, … için  eşitliği sağlanır. eşitliği sağlanır.Euler dönüşümü 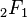 hipergeometrik dizisine sıklıkla uygulanmkatadır. Bu durumda Euler dönüşümü hipergeometrik dizisine sıklıkla uygulanmkatadır. Bu durumda Euler dönüşümü olarak ifade edilebilmektedir. olarak ifade edilebilmektedir.Binom dönüşümü ve bunun farklı bir uyarlaması olan Euler dönüşümü bir sayının sürekli kesir olarak ifade edilmesinde büyük önem taşımaktadır. 0 < x < 1 sayısının sürekli kesir ifadesinin  olduğu varsayılsın. olduğu varsayılsın. Buradan  ve ve sonuçlarına ulaşılabilmektedir. sonuçlarına ulaşılabilmektedir.Üstel üretici işlev Üstel üretici işlev için  ve ve eşitliklerinin sağlandığı varsayılsın. Buradan eşitliklerinin sağlandığı varsayılsın. Buradan eşitliğine ulaşılır. eşitliğine ulaşılır.Borel dönüşümü, olağan üretici işlevi üstel üretici işleve dönüştürebilmektedir. İntegral biçimindeki ifadesi Dizi bir karmaşık çözümleme işleviyle değiştirildiğinde dizinin binom dönüşümü Nörlund-Rice integrali biçiminde ifade edilebilmektedir. Genellemeler Prodinger birimsel benzeri bir dönüşümden söz etmektedir.  eşitliğinin sağlandığı varsayıldığında eşitliğinin sağlandığı varsayıldığında ifadesine ulaşılır. Burada U ve B sırasıyla {un} ve {bn} dizileriyle ilişkilendirilmiş olağan üretici işlevleri göstermektedir. ifadesine ulaşılır. Burada U ve B sırasıyla {un} ve {bn} dizileriyle ilişkilendirilmiş olağan üretici işlevleri göstermektedir.Artan k-binom dönüşümü zaman zaman  biçiminde, azalan k-binom dönüşümü biçiminde, azalan k-binom dönüşümü biçiminde tanımlanmaktadır. Her iki dönüşüm de bir dizinin Hankel dönüşümü özüne eşittir. biçiminde tanımlanmaktadır. Her iki dönüşüm de bir dizinin Hankel dönüşümü özüne eşittir.Binom dönüşümü 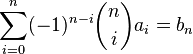 olarak tanımlanır, bu ifade olarak tanımlanır, bu ifade işlevine eşitlenir, yeni bir ileri fark tablosu oluşturulur ve bu tablonun her satırının ilk elemanından {bn} gibi yeni bir dizi oluşturulursa özgün dizinin ikinci binom dönüşümü  ifadesine eşit olur. ifadesine eşit olur.Aynı işlem k kez yinelendiğinde 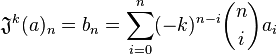 eşitliğine ulaşılır. Bu ifadenin tersi eşitliğine ulaşılır. Bu ifadenin tersi olarak yazılır. olarak yazılır.Bu ifadenin genel biçimi  olarak yazılabilir. Burada olarak yazılabilir. Burada 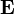 değişim işlecini göstermektedir. değişim işlecini göstermektedir.Bu ifadenin tersi  biçiminde gösterilir. biçiminde gösterilir. --------------Tualimforum İmzam-------------- Aksini Belirtmediğim Takdirde Yazdığım Konular ALINTIDIR Liseler - Anadolu Liseleri - Fen Liseleri Anaokulu - İlköğretim Sınav Soruları ve Ders Notları | |||
| |  |