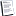| |  Digama Fonksiyonu
Digama Fonksiyonu Matematik'te, digama fonksiyonu gama fonksiyonu'nun logaritmik türevi olarak tanımlanır:
Bu poligama fonksiyonu'nun ilkidir.
- kompleks düzlem'de ψ(s) Digama fonksiyonu renkli bir s noktasına karşı kodlanan değer ψ(s). Güçlü renkler sıfıra yakın değerleri ve tonları gösteren ise argument değerleridir.
Harmonik sayılar ile ilişkisi
Digamma fonksiyon'u, sıklıkla ψ0(x), ψ0(x) veya  (eski yunan harfleriyle digama'nın gösterimi Ϝ'dir ) şeklinde gösterilir. Harmonik sayılar'la ilişkisi
Burada Hn is the n 'inci harmonik sayıdır, ve γ Euler-Mascheroni sabiti'dir. yarı tamsayı değerleri için, açılım
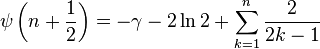
Integral Gösterimleri
integral gösterimi
 şeklindedir.
x reel kısmının pozitif değerleri için geçerlidir.Bunu şöyle yazabiliriz
harmonik sayılar için Euler integrali'dir .
Seri formülü
Digamma negatif tamsayılar dışında kompleks düzlemde hesaplanabilir (Abramowitz and Stegun 6.3.16), yardımıyla
Taylor serisi
Digama Taylor serisi'nde z=1 verilerek elde edilen bir rasyonel zeta serisidir , . Burada
yakınsaklık için |z|<1. Burada, ζ(n) Riemann zeta fonksiyonu'dur.Bu seri ile kolayca Hurwitz zeta fonksiyonu'na karşılık gelen Taylor 'serisi elde edilebilir.
Newton serisi
Digama için Newton serisi Euler integral formulü ile :
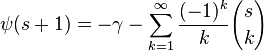
Burada  binom katsayısı'dır
Refleksiyon formülü
Digama fonksiyonunu Gama fonksiyonu'na benzer bir refleksiyon formülü karşılar
Özyineleme formülü
tekrarlama ilişkisi'ne dayanılarak Digamma fonksiyonu
Böylece,1/x için "teleskop" denilebilir , bu nedenle
Burada Δ ileri diferansiyel operator'dür. Aşağıdaki formülle harmonik seri'nin kısmi toplamı tekrarlama ilişkisi'ne karşı gelir ,
burada  Euler-Mascheroni sabiti'dir.
Daha genel bir ifade,
Gauss toplamı
Digama'nın Gaussian toplam formu
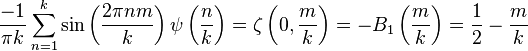
Tamsayılar için 0 < m < k. Burada, ζ(s,q) Hurwitz zeta fonksiyonu'dur ve Bn(x) 'i Bernoulli polinomu'dur.Çarpma teoremi'nin özel bir durumu ;
ve genelleştirilmiş şekli
Burada q 'nun doğal sayı, ve 1-qa 'nın doğal sayı olmadığı varsayılmıştır. .
Gauss'un digama teoremi [
Pozitif tamsayılar m ve k ( m < k ) şartıyla,digama fonksiyonunun Temel fonksiyon olarak ifadesi
Hesaplama & yaklaşıklık
J.M. Bernardo AS 103 algoritmiyle ile x, gerçel bir sayı olmak üzere digama fonksiyonu hesaplanabilir,
 veya
n tamsayı, B(n) n 'inci Bernouilli sayısı ve ζ(n) Riemann zeta fonksiyonu'dur.
Özel değerler
Digama fonksiyonu için bazı özel değerler:
 |
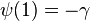